已知正多边形内角度数则其边数为：360°÷（180°－内角度数）

推论

任意正多边形的外角和=360°

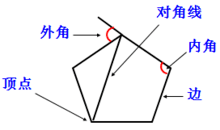
正多边形任意两条相邻边连线所构成的三角形是等腰三角形

多边形的内角和

〔n-2〕×180°（n为边数）

多边形内角和定理证明

证法一：在n边形内任取一点O，连结O与各个顶点，把n边形分成n个三角形.

因为这n个三角形的内角的和等于n·180°，以O为公共顶点的n个角的和是360°

所以n边形的内角和是n·180°-2×180°=（n-2）·180°.（n为边数）

即n边形的内角和等于（n-2）×180°.（n为边数）

Specialized polyhedral dice for role-playing games

证法二：连结多边形的任一顶点A1与其不相邻的各个顶点的线段，把n边形分成（n-2）个三角形.

因为这（n-2）个三角形的内角和都等于（n-2）·180°（n为边数）

所以n边形的内角和是（n-2）×180°.

专业多面体骰子在木制 sur 上角色扮演游戏

证法三：在n边形的任意一边上任取一点P，连结P点与其不相邻的其它各顶点的线段可以把n边形分成（n-1）个三角形，

这（n-1）个三角形的内角和等于（n-1）·180°（n为边数）

以P为公共顶点的（n-1）个角的和是180°

所以n边形的内角和是（n-1）·180°-180°=（n-2）·180°.（n为边数）

重点：多边形内角和定理及推论的应用。

难点：多边形内角和定理的推导及运用方程的思想来解决多边形内、外角的计算。