2.1电机相关物理量

电机是一个运动部件，要对电机进行控制，首先需要了解电机远动相关的物理量，包过位置，转速，加速度，力矩等。对电机的控制好坏，最终控制的就是电机力矩的精细程度。因此，有必要对相关知识进行回顾。

2.1.1角位置θ

物体的角位置是相对于某一任意参考点所测得的，其所旋转的角度。角位置通常用弧度或者度来计量 。角位置与沿某一直线的线性距离概率相对应。

2.1.2角速度ω

角速度或者转速是角位置随时间变化的速率。如果逆时针旋转则为正，顺时针旋转则为负。角速度是沿直线速度概念的旋转比拟。角速度定义为角位置随时间的变化率，如下：

ω=dθ/dt

如果角位移的单位是弧度（rad），则角速度用速度每秒（rad/s）来计量。在处理常规电机时，我们通常不用弧度每秒来作为单位来描述转轴速度，转速常以转每秒（r/s）或者转每分（r/min）给出。因为转速在电机的研究中非常重要，所以，当用不同的单位表示转速时，习惯上采用不同的转速符号。常用下列符号来描述角速度：

ωm:弧度每秒表示的角速度

fm:转每秒表示的角速度

nm:转每分表示的角速度

这些符号中的下标m表示为机械量，以与电气量相区别。如果不存在电气量与机械量的区别，则可以省去。他们之间的相互转化关系如下：

nm=60fm

fm=ωm/2π

2.1.3角加速度α

角加速度是角速度随时间变化的速率。从代数意义上看，所过加速度是增加的，则假定角加速度为正。角加速度是沿直线加速度概念的旋转比拟。公式为：

a=dω/dt

如果角速度的单位是弧度每秒（rad/s），则加速度用弧度每秒平方（rad/s²）来计量。

2.1.4转矩τ

直线运动中，给物体施加力会引起其线速度改变。如果物体上没有净作用力，则其速度恒定不变。施加到物体的力越大，则其速度的改变越迅速。

对于旋转运动也有类似的概念。当物体旋转时，除非其上出现转矩，否则其角速度将恒定不变。物体上作用的转矩越大，则该物体角速度的改变越迅速。

什么是转矩？转矩可以宽泛的称为作用在物体上的“扭转力”。它的转矩定义为：施加到物体上的力与力作用线与物体旋转轴线最小距离的乘积。

τ=所施加的力X锤子距离

=(F)(rsinθ)=rFsinθ

其中，F为所施加的力，r力作用线到物体旋转轴线的垂直距离，θ为夹角。转矩单位为牛.米即N.m。

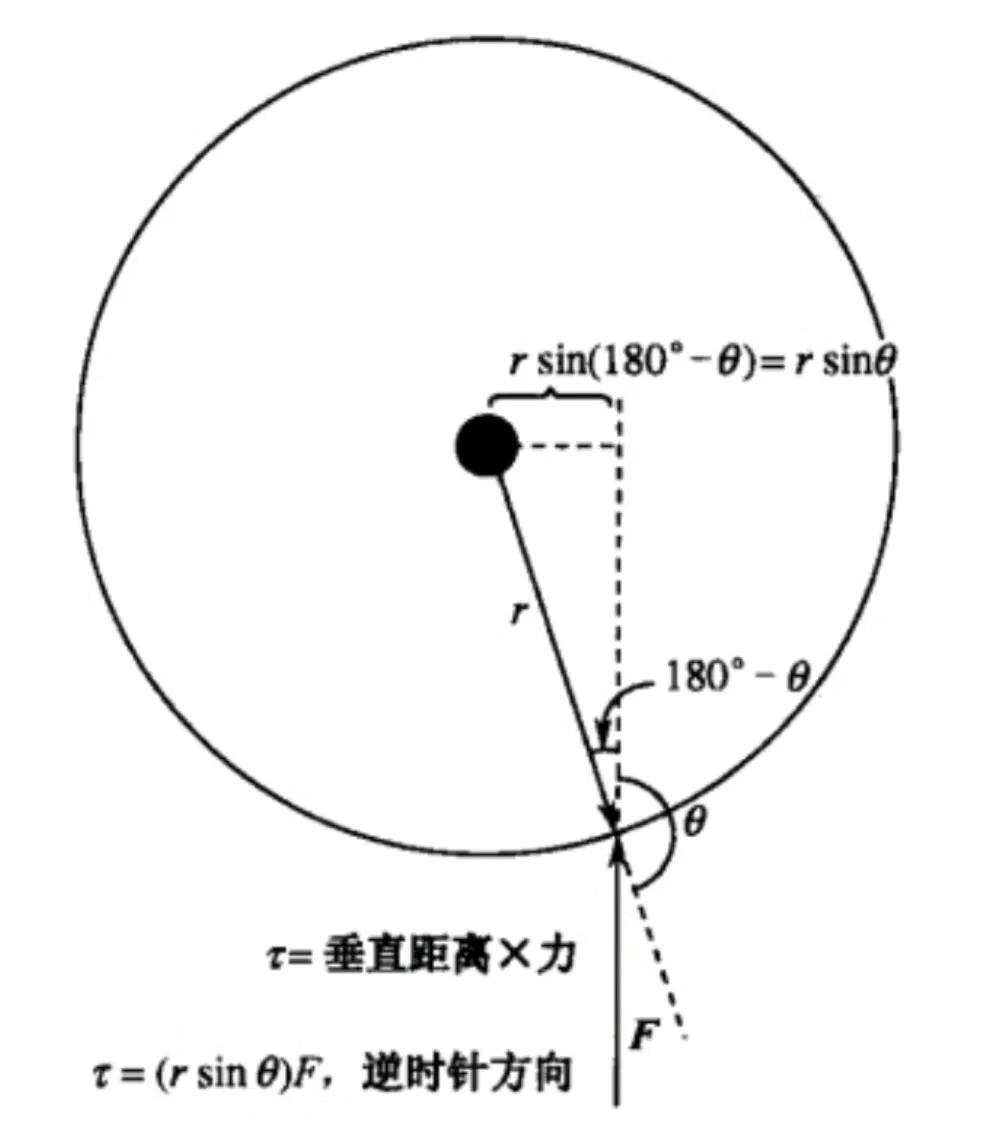
图一 物体上转矩表达式的推导

2.1.5牛顿旋转定律

我们知道，对于直线运动，施加到物体上的力与加速度的关系有：

F = ma

用类似的表达式描述施加到物体上的转矩和其所产生的角加速度之间的关系。此关系称为牛顿旋转定律，如下所示：

τ=Ja

式中，τ为所施加的转矩，单位牛.米，a为产生的角加速度，单位为弧度每平方，J称为物体的转动惯量，可以与物体的质量类比来看，单位为千克.米平方（kg.m²）。

2.1.6 功W

对于直线运动，功定义为力作用在物体上使其移动一段距离。表达式如下：

W = Fr

式中，W 为功，F为作用在物体上的力，r为移动的直线距离。

对于旋转运动，功定义为转矩作用在物体上使其转过一定角度。表达式如下：

W=τθ

式中，W为功，τ为作用在物体上的转矩，θ为转过的角度。

2.1.7功率P

功率是做功的速率或者单位时间功的增量。功率的表达式为：

P=dW/dt

功率通常用焦耳每秒（瓦，W）来计量。

根据此定义，假设力为恒定值并与运动方向在同一直线上，则：

P=dW/dt=d(Fr)/dt=Fdr/dt=Fv

类似地，假设转矩恒定，则得出旋转运动的功率为：

P=dW/dt=d(τθ)/dt=τdθ/ft=τω

此式在电机学中非常重要，需要熟记，因为其可以描述电动机转轴上的机械功率。