角平分线是初中数学中最重要几种线之一，在中考中属于必考知识点。角平分线本身涉及的知识点不多，比较容易理解和掌握，难度不大。

1.定义：把一个角平均分成大小相等的两个角的一条射线。

• 分析定义：在做题中，看到角平分线，首先就需要联想到相等的角，2倍角和1/2角的关系。

2.性质定理：角平分线上的点到角两边的距离相等。

• 角平分线的性质定理是考试必考知识点，过角平分线上的点向角两边做垂线是角平分线中最常用的辅助线。

3.判定定理：到角两边距离相等的点在角平分线上。

• 角平分线的判定定理是判断一条射线是否是某个角的角平分线的方法，也是证明点在线上常用的方法。

4.内心：三角形三条角平分线的交点称为这个三角形的内心。

• 三角形的内心也就是三角形内切圆的圆心。画三角形的内切圆，只需要作出三角形的两条角平分线，交点位置即为圆心，过交点向任意边作垂线，垂线段的长度即为内接圆半径。

除了这些基本的知识点外，在考试中角平分线通常涉及到以下常用的几何模型，综合性强一些，掌握常见的几何模型可以帮助我们提高做题速度和效率。

1.三角形两内角角平分线：

三角形两内角角平分线：

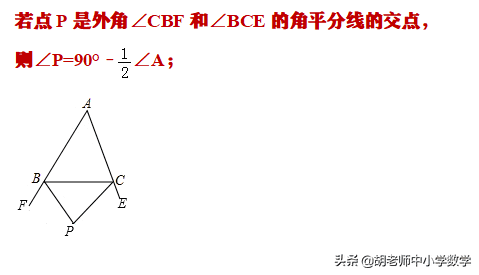
2.三角形内外角角平分线：

三角形两外角角平分线：

3.三角形两外角角平分线：

4.角平分线＋平行线→等腰三角形：

角平分线＋平行线→等腰三角形：

5.过角平分线上的点作角两边的垂线：

过角平分线上的点作角两边的垂线：

6.角平分线的两端过角的顶点取相等的两条线段构造全等三角形：

取相等的两条线段构造全等三角形

7.过角平分线上一点作角平分线的垂线，从而得到等腰三角形：

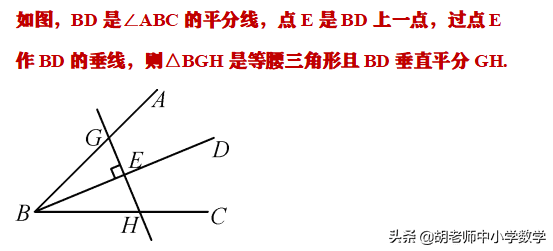
过角平分线上一点作角平分线的垂线

七道例题，每道例题对应相应的模型：

模型是在掌握基础知识点、方法和思路基础之上的提炼和升华，是经验的总结和积累，掌握常用的几何模型可以帮助我们快速找到解题的思路和方法，提高解题效率。可运用模型，但不能依赖模型，对几何模型的学习和掌握必须要深入，需要掌握其来源、原理、适用条件和范围等等。

在这七种模型中，运用最多的要数第四和第五种，尤其是第五种，基本是逢考必考，过角平分线上的点向角两边作垂线是几何中常用的辅助线之一，在解题中要有这种做辅助线的意识，看到角平分线，过上面的点向两边作垂线。