一、实数与向量的积的运算律：设 λ、μ 为实数，那么：

① 结合律：

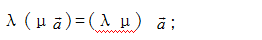
结合律图

② 第一分配律：

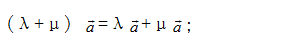
第一分配律图

③ 第二分配律：

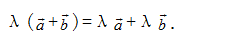
第二分配律图

二、向量 a 与 向量 b 的数量积(或内积)：

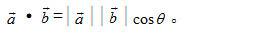
数量积图

三、平面向量的坐标运算：

①

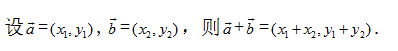
平面向量的坐标运算图（1）

②

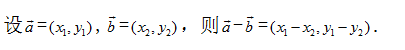
平面向量的坐标运算图（2）

③

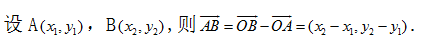
平面向量的坐标运算图（3）

④

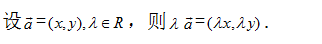
平面向量的坐标运算图（4）

⑤

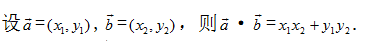
平面向量的坐标运算图（5）

四、求夹角和长度：

① 求夹角：

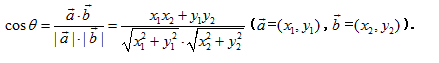
求夹角图

② 求长度：

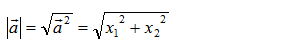
求长度图

五、平面两点间的距离公式：

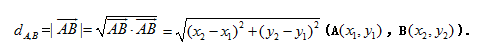
平面两点间的距离公式图

六、共线向量定理：

空间任意两个向量

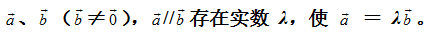
共线向量定理图

① 三点共线：

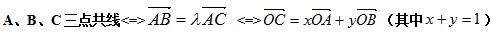
三点共线图

② 与 向量 a 共线的单位向量为

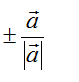
与 向量 a 共线的单位向量图

七、共面向量：

① 定义：一般地，能平移到同一平面内的向量叫做共面向量。

说明：空间任意的两向量都是共面的。

② 共面向量定理：

共面向量定理图

③ 四点共面 ：

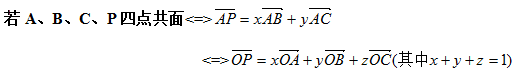
四点共面图

八、向量的平行与垂直 ：

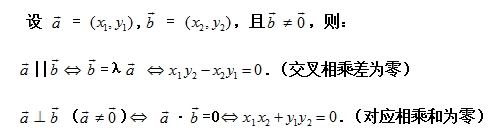
向量的平行与垂直图

九、线段的定比分点公式 ：

线段的定比分点公式 图

十、三角形的重心坐标公式：

△ABC三个顶点的坐标分别为 A（x1 , y1）、B（x2 , y2）、C（x3 , y3）, 则 △ABC 的 重心 的坐标是

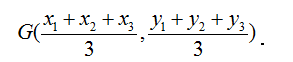
三角形的重心坐标公式图

十一、三角形四“心”向量形式的充要条件：

设 O 为 △ABC 所在平面上一点，角 A , B , C 所对边长分别为 a , b , c ，则

①

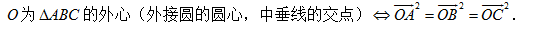
三角形四“心”向量形式的充要条件图（1）

②

三角形四“心”向量形式的充要条件图（2）

③

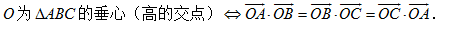
三角形四“心”向量形式的充要条件图（3）

④

三角形四“心”向量形式的充要条件图（4）