什么是转动惯量
转动惯量是一个物理量,它描述了物体绕给定轴旋转的容易程度。它是质量的旋转模拟,描述了物体对平动的阻力。惯性是物质抵抗运动状态变化的特性。惯性是一种力的度量,它使静止的物体保持静止,或使运动的物体以当前速度运动。惯性越大,在给定时间内使其速度发生变化所需要的力就越大。假设一个重型卡车和一盏灯的车都处于静止, 然后直觉上我们知道将需要更多的力量推动卡车一定的速度在一个给定的时间比需要推动汽车, 在相同的时间相同的速度。
类似地,惯性矩(转动惯量)是物质在旋转运动状态下抵抗变化的特性。转动惯量越大,在给定时间内使其角速度发生相同变化所需要的转矩就越大。这里,力矩和角速度是力和速度的类比,与转动惯量有关,就像力和速度与质量的关系一样。
不像惯量,转动惯量不仅取决于质量还取决于绕轴的质量分布。物体在不同的轴上可以有不同的转动惯量。也就是说,要使一个物体以相等的角加速度绕不同的轴旋转,就需要不同的力矩。在整个机制中,这一概念是相关且非常必要的。虽然如果没有旋转,生活会很简单,但实际上我们需要有一种方法来处理平移和旋转(通常是同时进行)。这是分析更复杂运动的必要部分。
关于转动惯量的计算
转动惯量不仅基于物体的物理形状和质量分布,还基于物体旋转的方式。所以同一个物体以不同的方式旋转会有不同的转动惯量。
01
一般计算公式
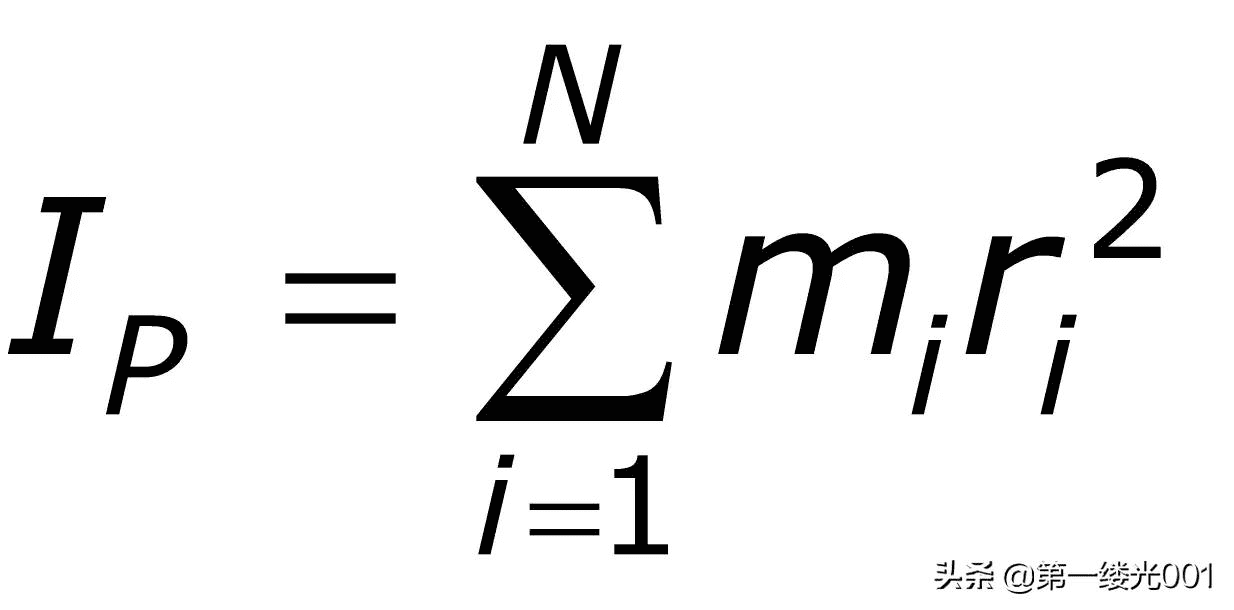
求转动惯量的一般公式。
一般公式代表了对转动惯量最基本的概念理解。基本上,对于任何旋转的物体,转动惯量可以通过取每个粒子到旋转轴的距离(方程中为r),平方这个值(即r2项),再乘以粒子的质量来计算。对所有组成旋转物体的粒子都这样做,然后把这些值加起来,就得到了转动惯量。
这个公式的结果是同一个物体得到不同的转动惯量值,这取决于它的旋转方式。即使物体的物理形状保持不变,新的旋转轴也会得到一个不同的公式。
这个公式是计算惯性矩的最“强力”的方法。所提供的其他公式通常更有用,代表了物理学家遇到的最常见的情况。
02
积分公式
一般公式是有用的,如果对象可以被视为一个离散点的集合,可以加起来。然而,对于一个更复杂的物体,可能需要应用微积分对整个体积进行积分。变量 r 是点到转轴的半径向量:
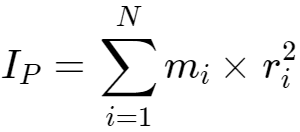
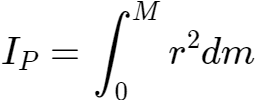
03
实心球体
一个实心球体,其质量为M,半径为R,沿穿过球体中心的轴旋转,其转动惯量由以下公式决定:
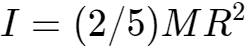
04
空心薄壁球
一个空心球体,它有一层可以忽略的薄壁,绕着穿过球体中心的轴旋转,质量为M,半径为R,其转动惯量由以下公式决定:
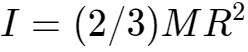
05
实心圆柱体
一个固体柱体,在一个穿过柱体中心的轴上转动,质量为M,半径为R,其转动惯量由公式决定:
I = (1/2)MR^2
06
空心薄壁圆筒
一个空心圆柱体,其壁很薄,可以忽略不计,沿穿过圆柱体中心的轴旋转,质量为M,半径为R,其转动惯量由公式决定:
I = MR^2
07
空心圆柱体
一个空心圆柱体,其质量为M,内半径为R1,外半径为R2,在穿过圆柱体中心的轴上旋转,其转动惯量由公式决定:
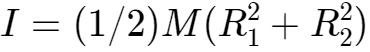
注:利用此公式,将R1 = R2 = R(或者更恰当地,取R1和R2接近公共半径R时的数学极限),就可以得到空心薄壁圆柱的转动惯量公式。
08
矩形板,轴穿过中心
一个矩形薄板,质量为M,边长为A和b,沿垂直于板心的轴旋转,其转动惯量由下面的公式决定:
I = (1/12)M(a^2 + b^2)
09
矩形板,沿边轴
一个薄的矩形板,沿板的一个边沿轴线旋转,质量为M,边长为A和b,其中A是垂直于旋转轴的距离,其转动惯量由下列公式决定:
I = (1/3)Ma^2
10
细长杆,轴穿过中心
一根细杆,其质量为M,长度为L,绕着穿过杆心(垂直于杆长)的轴旋转,其转动惯量由公式决定:
I = (1/12)ML^2
11
细长杆,轴通过一端
一根细杆,其质量为M,长度为L,绕穿过杆端(垂直于杆长)的轴旋转,其惯性矩由公式决定:
I = (1/3)ML^2
