人教版八年级上学期——直角三角形30°角性质及其变式拓展

直角三角形30°角性质：直角三角形30°角所对的直角边等于斜边的一半.

如图，在Rt△ABC中，∠C=90°，∠A=30°，则CB=1/2AB.

接下来，我们重点研究下与直角三角形30°角有关的变式：

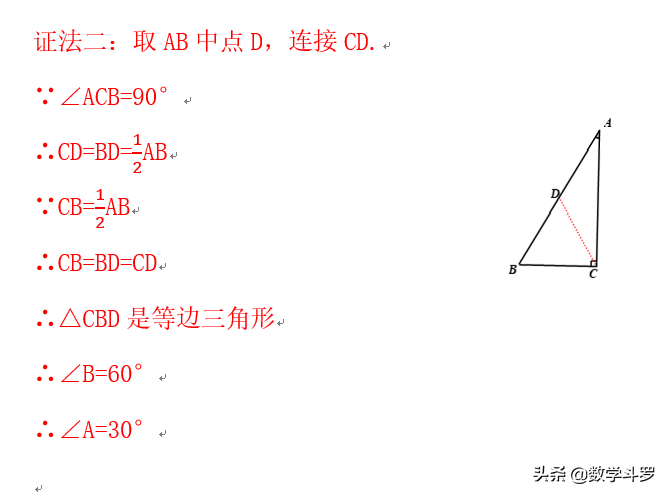
变式1：

在Rt△ABC中，∠C=90°，CB=1/2AB，则∠A=30°.

变式2：在三角形ABC中，∠B=60°，BC=1/2AB，则∠ACB=90°.

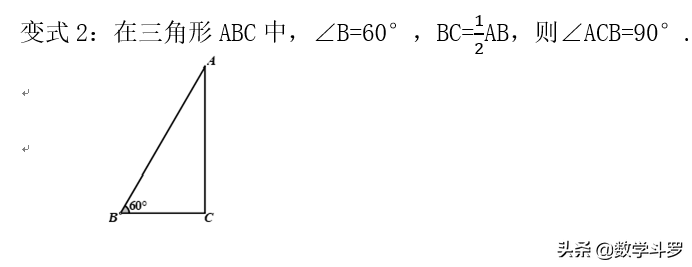
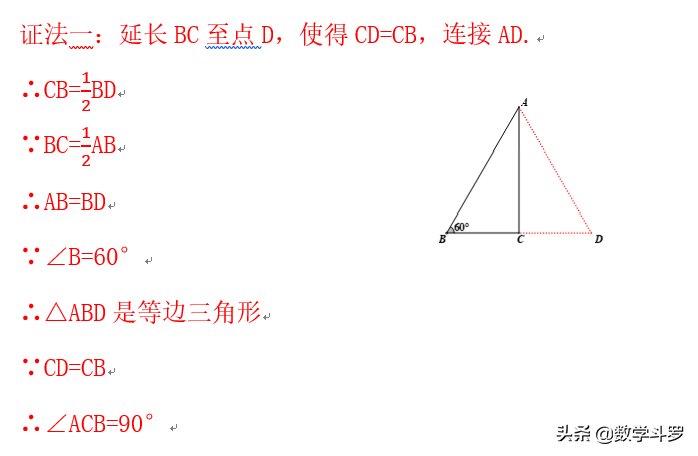
结语：变式1和变式2的证明，不论是法一的倍长中线法，还是法二的取中点连接法，都是为了构造等边三角形.变式1在初二阶段很多时候都被模糊化处理（初三会学习锐角三角函数）.但笔者认为不妥，我们不能说初三要学就刻意回避它，不给其以合理解释。

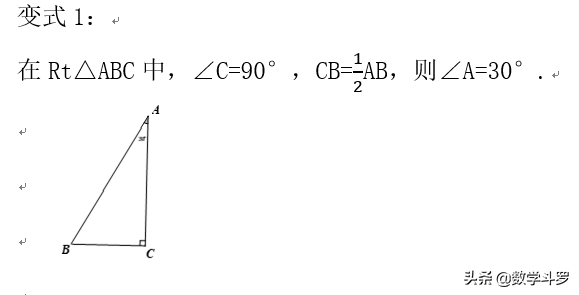
变式二应用：

如图①，O为正方形ABCD的中心，分别延长OA，OD到点F，E，使OF=2OA，OE=2OD，连接EF，将△EOF绕点O逆时针旋转α角得到△EOF（如图②）.

（1）探究AE1与BF1的数量关系，并给予证明；

（2）当α=30°时，求证：△AOE1为直角三角形.