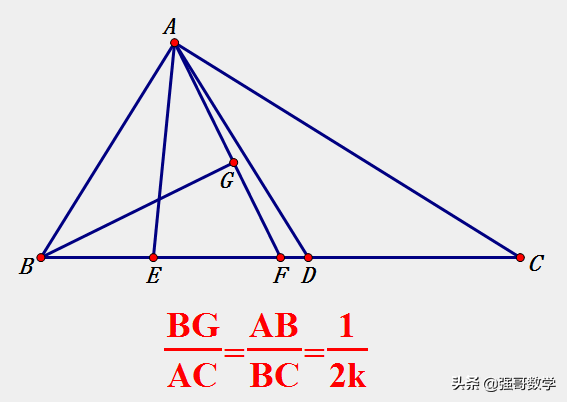
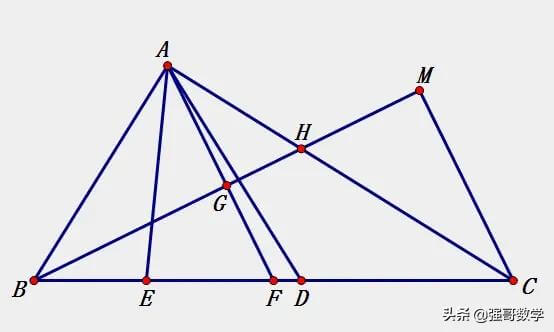
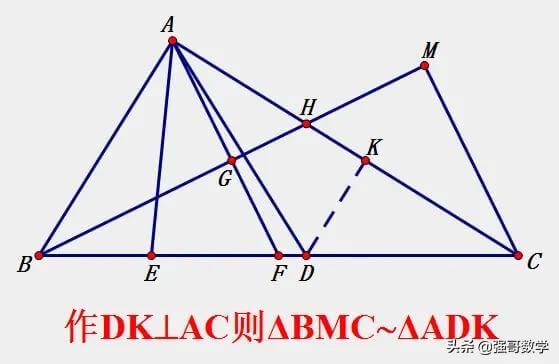
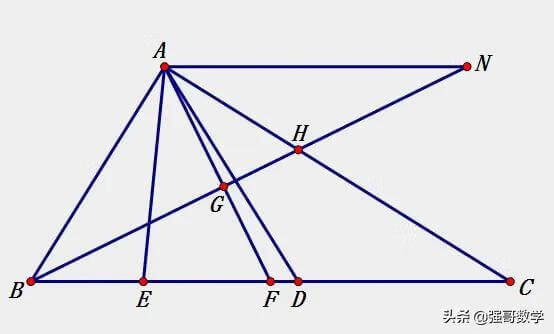
在上一篇文章里,细心的读者会发现如下几个规律性的解题认知:
一边一角构造全等三角形模式
等腰三角形构造轴对称或者旋转式儿全等
二倍角转化,通常都是小角扩大二倍
下面,我们来看看2019年大连市25题,不知道它又能给我们在解决几何压轴题里,添加什么有用的新东西。
2019年大连市25题

人的思虑太甚,肯定要累成狗
凡是数学题里,出现类似于本题条件中,括号部分给出的k的取值范围:√2/2 这样的条件,常常都能给做题者浑身来个激灵,对唯恐漏掉一个细节的担心,促使做题者去想,这样的条件到底有什么用呢? 其实,本来就没什么用。 这样的条件,只是出题者为了保证题目的科学性,而有的画蛇添脚之笔。原本题目开始的如图两个字,就已经保证了所有,怎么可能还会有问题呢? 担心担心再担心,直接累瘫! 这是一条不成文的规定。 由条件:∠ABC=∠ACB+∠BAE去倒角,只要进行类似于解方程中的移项步骤: ∠ABC-∠ACB=∠BAE 再来个条件AB=AD得出∠ABC=∠ADB就齐活了。 问题是,为什么要让人如此的费劲儿呢?这个简单,就是出题者要了解一下你的基础,尤其是初一基础,再没有别的原因。有人不是常常放言,后两道题不是一般人能做的吗?出题者现在这么安排了,是不是特别一般的学生,也能拿下这个问题的分了? 擎好吧您! 如果这两个三角形,需要有一条边重合的话,那么,其中一个三角形的第三个顶点,就只能被要求在另一个三角形的另外两条边上。 综合考虑其全部情况,会有如下四种可能: 1.重合的两条边,一个是腰,另一个是直角边 如果等腰三角形的顶点与直角顶点重合,那么,两个三角形的第三个点,就只能在一条直线上。 本题就属于这种情况。 如果等腰三角形的顶点与斜边端点重合,那么,两个三角形的第三个点,就只能在斜边上。 2.重合的两条边,一个是腰,另一个是斜边 如此形成的图形,有等腰三角形腰上高, 还有等腰三角形三线合一两种情形。 3.重合的两条边,一个是底,另一个是直角边 形成的图形,是直角三角形斜边中线的情形。 4.重合的两条边,一个是底,另一个是斜边 形成的图形,是等腰三角形的顶点,在一个直角三角形的一条直角边上。 等腰三角形中,腰和底满足关系式: BD=2ABcos∠ABC。 再给条件:AB=kBD。 ∠ABC就是已知。 而一个锐角已知的直角三角形,其边之间的关系也就被确定了。 我们说,等腰三角形给出腰和底的比值,与给出一个内角或者其三角函数值,是一个意思。 如上事实,对另一个特殊的直角三角形,也是同样适用的。 所以,如果等腰三角形和直角三角形,按照如上的几种方式形成组合图形,就可以进行这种链式传递思考。 为根本解决问题⑵⑶,我们进行如下一般性说明,由此,说明过程就是解决问题⑵⑶的过程。 考虑到全等是一种特殊的相似「相似比为1」,我在本文里,就以相似为主,来谈两条线段的数量关系,希望大家注意。 从位置上观察,两条线段有如下三种情况 第一种情况,通常作平行线和垂线,也可以考虑面积法。这种情况,也是本题第⑶问的情况,我留待下面去说明。 第二种情况,考虑作垂线,以及等边对等角,还有旋转和轴对称全等。 至于第三种,也是本题的情况,就可以考虑做为相似三角形的两条对应边,以及都用某一个字母「作为题目中,已经设好的线段长」表示来思考了。 本题中,要求的两条边,所在的三角形是 △ABG和△ABC 至于这两个直角三角形是否相似,我们只要找到他们的一组锐角: ∠BAG=∠ABC 而找这一组锐角,而不找另外一组锐角,全在于锐角∠ABG是最后才生成的原因。 思考问题⑵至此,其他条件如角平分线,以及可用的问题⑴结论了,就都一下子呼之欲出,整个问题就变得自然流畅得来全不费工夫了 如果如上的第一个步骤,是为了找出结论中的线段所在的两个三角形相似,那么,现在我们所说的第二个步骤,就是再利用相似三角形的性质,把这两条线段之比,转化为其他两条线段「姑且记为a和b」之比了。 对于上面的第3种情况,由上面的分析说明,我们知道a和b是AB和BC,还是比较容易理解的。 由此,我们得到本问题⑵的说明: 至于在上面的第1和第2两种情况中,如果你作了垂线,a,b就是这两条垂线段,如果你作了平行线,a,b就是这两条平行线段。 由此,我们得到本问题⑶的两个说明: 为便于说明,先设BD=x, 则AB=kx,BC=2k²x 问题⑶方法一:做垂线得 AH:HC=AG:MC 其中,由问题⑵的解决可知,AG可以用kx表示,但是要用kx表示CM,那就需要再作一条垂线了 问题⑶方法二:做平行线得 AH:HC=AN:BC 其中,AN要用kx表示,也得需要再找一组相似三角形才能够。角的条件给的烂,你就只能慢慢倒
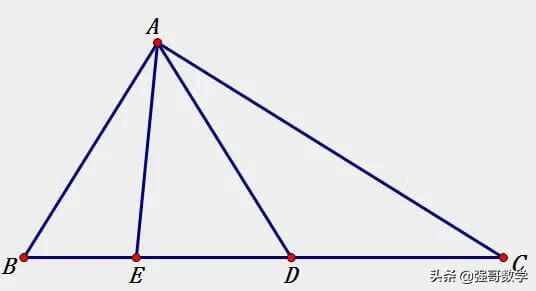
直角和等腰三角形的组合图形
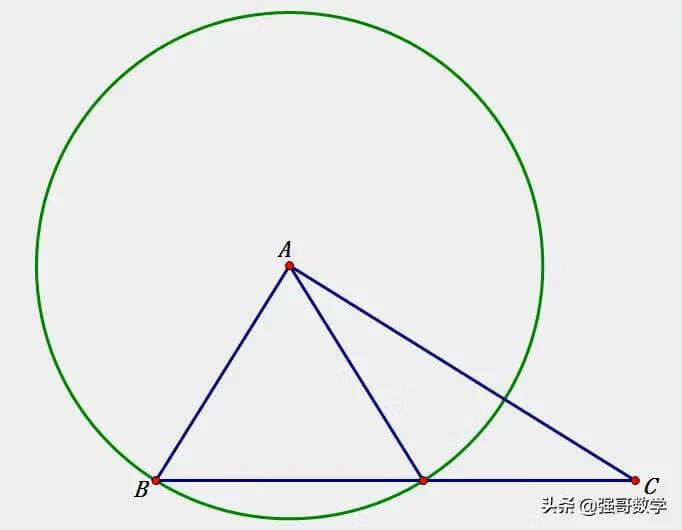
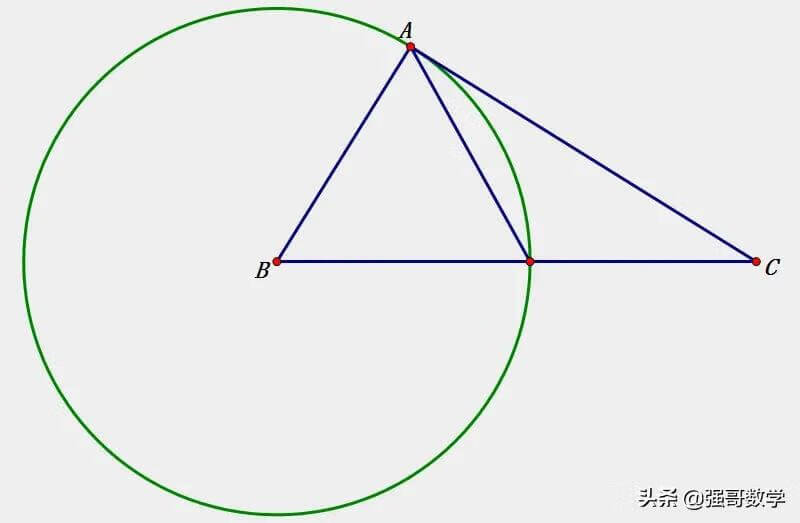
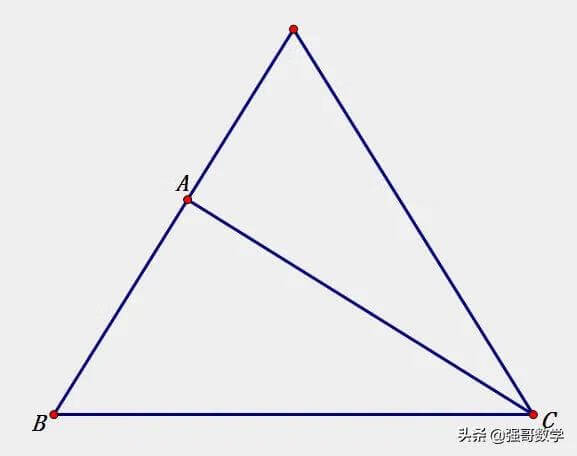
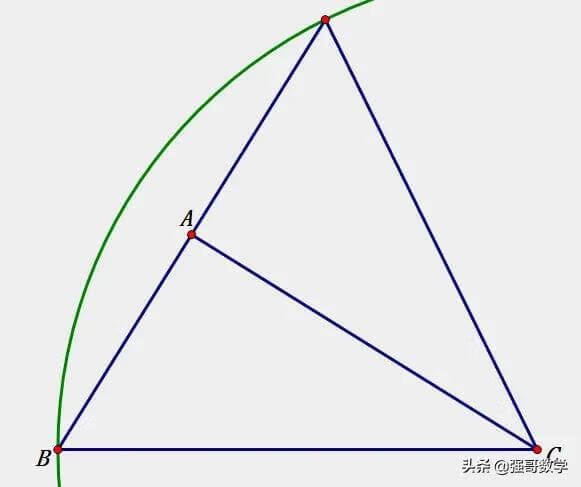
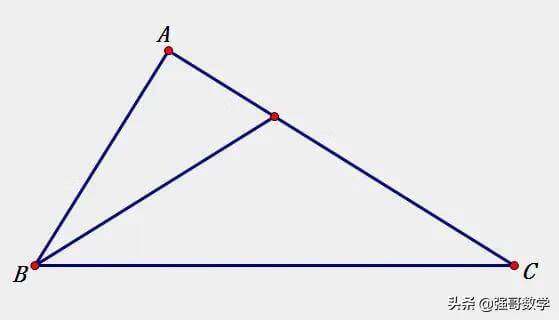
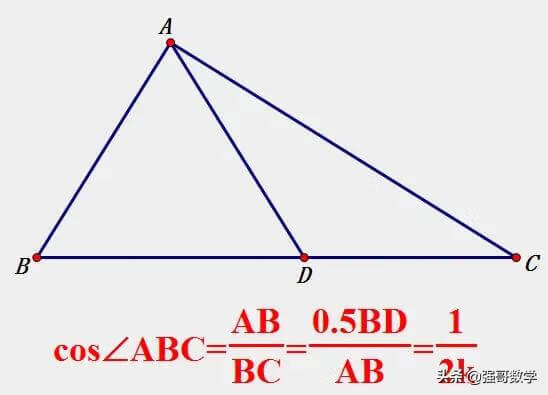
思考两条线段数量关系的第一个步骤
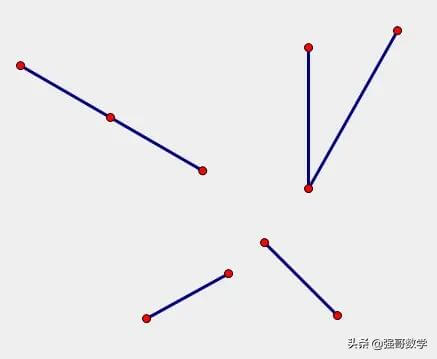
思考两条线段数量关系的第二个步骤